Curriculum Training for Physics-Informed PIC Code Surrogates

27 Aug, 2025

Staying DRY in Geneva

During my first (botched) attempt at a PhD, I came up with a few (to my mind) moderately-novel and interesting ideas for investigation at the increasingly-blurred interface between experimental physics and machine learning. During my time at CERN (more on that later) it's effectively impossible (or thermodynamically miraculous) to avoid the use of some form of neural net. When you consider the sheer magnitude and scale of even the SPS, who is the LHC's older and weaker brother, you quickly find yourself needing to turn to nets for either data analysis (traditional) or even optimising parameters for beam control and steering (exciting). Suffice it to say that, if you spend a week or two sitting in the main room of the CERN Control Centre for 18 hours [sic.] a day, someone will talk about "the neural net."

"The neural net." Which neural net, exactly? Good question. Working in the ML pipeline is, as many of us can attest, as much, if not more, of a function of feature engineering (deciding what goes into the network), architecture design (what type of net are you feeding things into, exactly?), and question-posing (what problem are you actually trying to solve?) as writing in CUDA C or scraping together a couple thousand lines of code. These questions are answered in reverse-cascading order; if you know what question you're trying to answer, you know what type of neural net will probably work best. If you know what neural net will work best, you probably know(ish) what you need to feed into it, etc.

There are many times you find yourself looking at a problem and having nothing more to go on than a sixth-sense itch that something isn't quite right. "It's 2025. Why am I doing this by hand? Why is anyone doing this by hand?" Probably the most important question to ask yourself. There's that famous old adage in coding, keep things DRY (Don't Repeat Yourself), which always bounces around my head when I'm looking at problems. In a world with pacemakers, several moon landings, running water, and ChatGPT, it stretches belief that one has to write a 4000-line Fortran-esque configuration by hand (or similar).

Plasma Physics is Messy. And hard. And weird.

In plasma physics, which, despite appearances, was technically the branch of physics I was working in last year (you would be forgiven, and not entirely wrong, to call me a particle physicist), you find yourself dealing with a few key problems. One: everything (or close enough to everything) is charged. This differs from things like water or air, where you often find charged species overwhelmingly outnumbered by neutral particles. Two: there are lots of particles. Specifically, a very large amount. It's a common joke at CERN that the whole LHC could be kept running for years on a bottle of hydrogen not much larger than a breadbox, and it's actually true. 1 mole is a dizzyingly large number of particles ( $~ 6 \times 10^{23}$ ), and you don't even come close to those numbers when you're working with beams at the LHC. In plasmas, you often have more "stuff" than would fit in a breadbox (at least one meant for human bread).

Fortunately, you have a couple of friendly caveats. One: Maxwell's Equations are linear (thank Christ). Two: people, past and present, were/are very smart (see caveat one). There are two competing descriptions of what goes on in a plasma: the fluid description, which is sort of easy to coarse-grain and work with in simulations, but is ultimately wrong (charged particles aren't as well-approximated by models of collective behaviour as neutral ones); and kinetic theory, which is, in principle, a complete and 100% accurate description of what is going on in the breadbox, but is incredibly difficult to implement on account of the requirement that you simulate all the particles (recall: 1 mole is really big). On top of this, you need to worry about things like magnetic and electric fields, which aren't a problem in neural fluids, but whose interplay with particles in a plasma is very complex. Moving charged particles produce both magnetic and electric fields. And they affect the fields around them. Which affects how they move. Which affects their fields... And so on.

This is where particle-in-cell (PIC) codes come in. Define some grid, which is fine-grained enough not to produce overly-naive and simplistic pictures of what's happening in the plasma, and which is coarse-grained enough that we can complete our calculations within the span of the age of the known universe. The coarse-graining produces approximations to the true dynamics and field strengths of the plasma by grouping together large numbers of smaller particles into some imaginary aggregate "super"- or "macro"-particle. Instead of computing the fields at every point in space and time (ideal), you calculate it everywhere on the grid. You fill in the spaces in-between by interpolating between these two points; the closer these points are together, the closer your interpolation will (probably) match reality, but more points equals more calculation, equals more computation. The grid shape, in 3D, will produce something that looks like a large number of cells with some macroparticles in them and... Well, on the spectrum of physicists' creativity in naming things, the name "particle-in-cell" falls closer to "streamline" than the "sneutrino".

The problem is that these codes are still incredibly cumbersome to use, and incredibly slow. One of my close friends (hi, R.D.!) spends a lot of their time running these codes, and ultimately extracting usable/presentable data from these codes. And it's slow. Usually, using PIC codes is more a function of choosing when to switch the thing off than wait for the end to come (it almost never does, even with moderately unambitious simulations on a high-performance cluster).

Physics-Informed Neural Networks

So this is where some of us out there in the world have started thinking about neural networks. Specifically, physics-informed neural networks (PINNs) which try to account for the underlying physics of a situation during the process of optimization.

Typically, loss functions are agnostic about the physics of what's going on. You often only specify some basic relationship between prediction and reality, and penalize deviation from this. In regression, this is often Mean-Squared Error (MSE) loss:

ℒ = \frac{1}{N} \sum_{i}^{N} {| y^{(i)} - {\hat{y}}^{(i)} |}^{2}

where we have some predicted value at a data point, ${\hat{y}}^{(i)}$ , and some "real" (ground truth) value at that data point, $y^{(i)}$ . Or, in multiclass classification problems, Cross-Entropy loss:

ℒ = - \frac{1}{N} \sum_{i}^{N} y^{(i)} \cdot log {\hat{y}}^{(i)}

where now the $y^{(i)}$ values are class labels, and ${\hat{y}}^{(i)}$ are typically the probability our model has assigned to data point $i$ belonging to that ground truth class.

You'll notice that there's no mention of any of the physics anywhere here. No fluid dynamics, no Maxwell's equations, no kinetic theory- only real labels or values, and predicted labels or values. So this is where Raissi comes in and starts talking about physics-informed loss functions, which encode the physics of our situation, and enforce penalties on the network for deviating from this physics. So now we have

ℒ_{fancy new} = λ_{o} ℒ_{old} + λ_{p} ℒ_{physics}

where we have introduced some "weights" on different parts of the loss, $λ$ , and where the physics part of the loss function is typically a sum of "residuals", or, simply put, how much our equation violates our models of physics, such as

ℒ_{physics, Newton} = \frac{1}{N} \sum_{i}^{N} | \frac{d^{2} x^{(i)}}{d t^{(i) 2}} - \frac{F^{(i)}}{m} |

Here, the introduction of an equation that in principle describes continuous time/space produces some extra complications regarding how we sample our points $x^{(i)}$ , but you can read about that somewhere else. What I've written above is just $F = m a$ , Newton's Second Law (for constant mass).

Introducing physics into the equation (is that a double, triple, quadruple pun?) has the additional benefit of restricting the set of possible solutions to the problem, or the size of the solution space, which means you need fewer training examples than ordinary in order to produce a decent model. Consider state-of-the-art image (convolutional neural net) classifiers, which are trained on tens of thousands (or more) images per class. If you want a CNN to reliably identify 10 different things, you're potentially looking at $100, 000$ images. PINNs offer the chance to get a huge discount on training dataset size.

So, we whack physics into the new loss function and carry on as normal. Right?

Well, not really. There are, you are probably aware, a few competing theories for how particles actually work. Indeed, in quantum mechanics (and, in quantum field theory, its most popular relativistic incarnation), there's actually no well-defined concept of a force, $F$ . Instead, "forces" as we perceive them are theorized to be the result of the exchange of gauge bosons (photons, the $W^{\pm} / Z$ weak gauge bosons, gluons). "Gravity", which is definitely a force for Newton, is currently not really considered a force at all (and the people who do think gravity is like the "other" 3 (or 2) forces have yet to locate a graviton, or formulate a renormalizable gauge theory of gravity...) Furthermore, if you don't want to go all the way down to relativistic quantum mechanics, you might want to instead enforce Schrödinger's equation, which only recognises wave-particle objects, and then and then and then and then...

And then the biggest problem: all theories of physics are approximations. This is what makes them useful, but also what makes them limiting: it's actually why we need computers in the first place, as only the most simple situations can actually be solved using pen-and-paper physics approaches (and even then, often with great difficulty).

This is where the first stage of the curriculum comes in. Some people out there who have experimented with this find that you can actually ramp up the physics slowly (e.g. add "more" Newton as needed) and start out with just the physics-less loss function. That's the situation where, in the equation above, $λ_{p}$ starts at $0$ and then increases.

PIC + PINN

The synthesis of these two concepts, PIC codes and PINNs, is as follows: choose your equations wisely (some combination of Navier-Stokes and Kinetic Theory), choose your neural net, and start churning out PIC code simulation data.

But wasn't it very expensive to produce PIC code simulations?

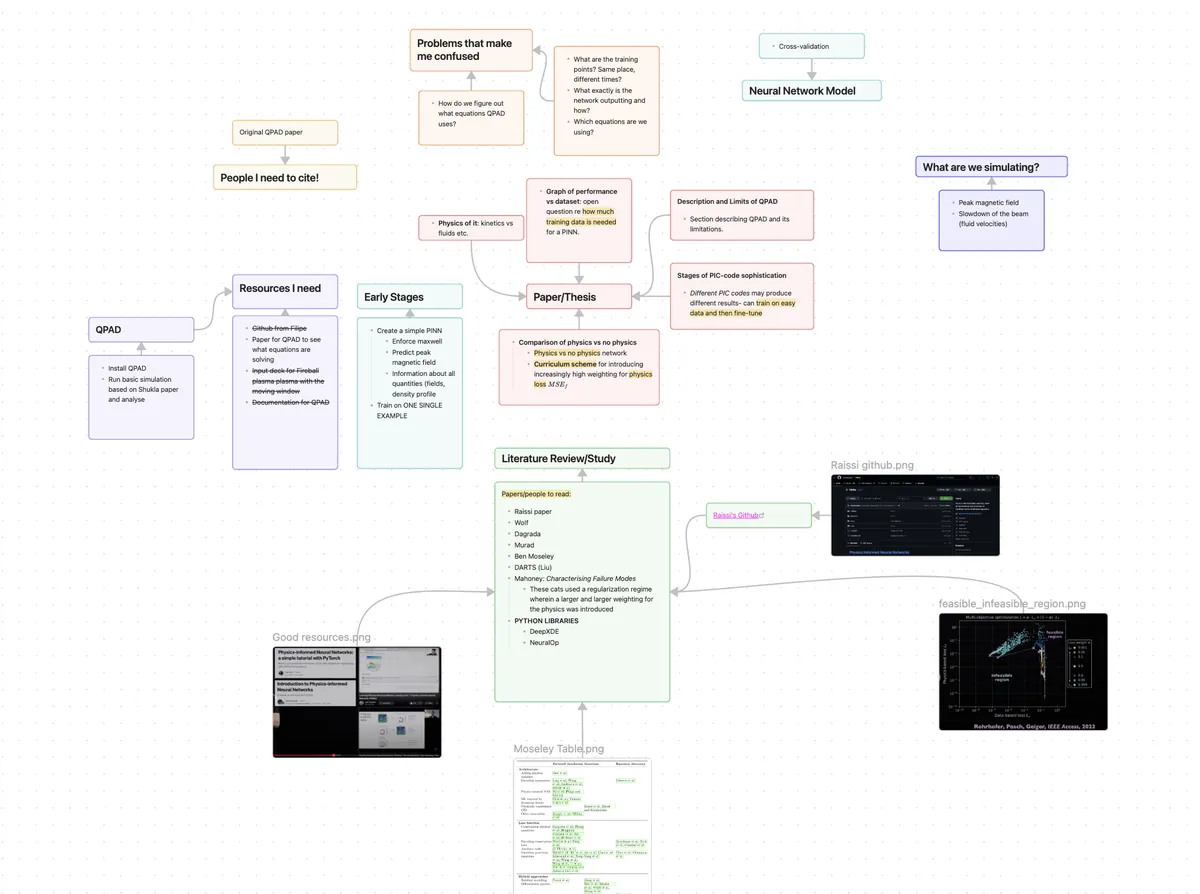Screenshot 2025-08-27 at 23 My original, early plan for this whole thing as a thesis. All for nothing, now.

This is where the second part of the curriculum was meant to come into things: we take some powerful dinosaur PIC code, like OSIRIS, and produce some small number of simulation data outputs (call it 20-50 across six-twelve months). Then, we go out and find some computationally-cheap code, which in our case was supposed to be QPAD, and just start turning the crank to produce as many decks of simulated data as possible. If possible, we interpolate these two degrees of complexity using some intermediate-level code, which is slower than QPAD but quicker than OSIRIS, and which produces data with higher granularity and/or accuracy than QPAD. QPAD compromises on the physics, but redeems itself in speed (and in many cases wasn't actually that bad of an approximation). Then, we train the network on a combination of the two, leveraging the larger volume of simplistic data to teach the network how plasmas generally behave, and then fine-tuning its knowledge using data of increasing sophistication. There was some hope/belief/indication/curiosity as to the network's ability to actually recreate physics it had never seen after training in this way, exploiting its knowledge from the smaller number of high-quality samples and a general fit to the data provided by things like QPAD.

Far-fetched as it may sound, this is actually what good neural nets do all the time. Take Stable Diffusion- it didn't have to have seen images of a lunar astronaut riding a horse (impossible for now in the 21st century) to generate one. Similarly, image classifiers and networks trained to make forecasting predictions by definition only have extrinsic value to the world and their users if they are able to identify, create, or predict data that it has never seen before. This is part-and-parcel with the generalization problem (how well do models do when they move beyond their training set), and is one of the most challenging parts of the whole chain. But they don't give out PhDs for solving problems someone else has already figured out. The hope was that we could go and take a look for ourselves.

Why?

Why bother? Well, there are a number of reasons, not least the problems of computational expense discussed earlier when it comes to these PIC code simulations. That in addition to the limited amount of high-performance computing space available to academics like my friend (hi again, R.D.!) who have to run dozens (or more) of these simulations every couple of months.

Neural network inference has the potential to be a lot faster. Even if a neural network is produced which fails to significantly beat the speed of state-of-the-art PIC codes, you can use distillation to produce smaller neural nets via a path that has no obvious analogy in traditional PIC code usage. These networks are smaller, faster, and can even identify things that they have never seen before simply by training on the knowledge of its parent network. In the Hinton paper I've linked above, they actually achieve $98.6 %$ accuracy on identifying images of the digit $3$ even when the smaller network has never been exposed to such a digit during training (they call this a "mythical digit"). There was some potential of us doing it here.

Conclusions and Sad Thoughts

I never actually got to implement the project as described. But someone- hopefully someone who is most acutely-aware of the pain of using PIC codes on a routine basis- can be motivated to try this out, and maybe this will be one of the few pokes or prods that gets them there.

Resistance and skepticism, both of which I encountered in abundance during the planning and proposal stage of the above skeleton plan, taught me a couple of things about research. One: everyone is worried about being replaced. We may not realise it, but it's what drives so many of us to being overly-skeptical and critical of the abilities of machine learning. And it makes sense- if you've spent twenty years learning how to ride a horse, what are you going to think about the cocky guy who pulls up past you in a Model T?

Additionally, we need to actually try new things. The whole point of academia is to do this. It pays (much) less, the lifestyle is demanding (some people work seven days a week, often not going home until long after everyone else would have, and even then, not always) and the field is competitive, which huge bottlenecks after your PhD. This has motivated everyone to prioritise measures of academic "virtue", like citation number, which inculcates in people a desire to gravitate towards what is easy, popular, or safe. No one wants to risk working five years on something only to find it never worked- people seldom cite papers titled "Why My All-Encompassing Theory of Gravity and Unicorns Never Worked", but nonetheless we should push ourselves to write those papers. Academia pushes people to stick other people's names on their papers even though those people did nothing to make the paper happen- all in the hope that they'll do the same for you one day, and all of you will languish in the "safe" part of the citation scale. It's immoral and intellectually dishonest, but it happens all the time, and it's perfectly rational given the system we've built for ourselves.

Hopefully someone out there reads this and agrees. Or maybe more than one. Only time can tell whether something works or fails, but success takes the longest when no one even tries.