Convolutional Denoising Autoencoders for Diagnostic Images

03 Sep, 2025

The Problem with Replicability (Motivation)

Developing new methods to process experimental data is a clear motivator for incorporating ML into physics. Indeed, data from physics experiments is messy- cameras exposed to radiation, time, and neglect can develop faulty or dead pixels in the active region of their CCDs. Upgrading and replacing these devices can be costly- so costly, in fact, that it's common practice to maintain damaged equipment across the years, rather than reinvest in something new all for the sake of a few humble yellow spots on a bitmap image. This makes sense if one of your primary expenditures is a specialist, ten-grand, several-kilowatt-strong radiofrequency (RF) power supply for, say, generating plasmas via inductive discharge (just a random example from the top of my head). It also makes sense if you have ways of dealing with these dead pixels which you are comfortable with and can explain in peer-review.

The problem is that most of what passes peer review should be rejected at preprint. If you critique common practices objectively, it's an Olympian feat of mental gymnastics to arrive at the conclusion that these methods are in any way satisfying. Namely, median filtering and Gaussian filtering, both of which wantonly discard real data in order to satisfy the aesthetic sensibilities of the physicist. In both of these cases, one is inevitably compromising on data. For the median filter, you are replacing pixels with the median value of their immediate neighbourhood. If your kernel-- the small matrix passing over your image which defines the operation; we'll get back to that later-- is too large, you're sacrificing too much data. Too small, and you fail to address even the problem you're crudely trying to solve- what is to happen when the kernel passes over some region of saturation that is larger than it? Furthermore, even if you can remove these isolated regions of abnormally high or low intensity, how are you to distinguish, with 100% reliability, these instances of saturation from experimental data?

For Gaussian filters, you're simply deciding that, above a certain frequency, the data doesn't matter- but what if your image has captured sharp edges? Plenty of high-frequency components there, I'm afraid.

You can solve some noise problems by producing a "flatfield"-- basically, take some "background" image in the absence of any interesting physics, and subtract this off from "real" images, but there are problems with this too¹. Or, you can just trust the filter. After all, it's what everyone else does.

When poring over a few thousand lines of one of my colleague's Python code, the problem of these approaches really clicked with me. Why is the frequency threshold on their Gaussian filter set to 123.4335235 and not 120? Why is the median filter using a kernel of this size? How do you know you're cutting out noise and not real data? Trial-and-error, was the answer. Proliferating throughout the code were a myriad "magic numbers"-- numbers that "just worked", but couldn't be justified in any replicable, scientifically-sound kind of way. In other words, every time someone comes to the table to do their own analysis, they have to reinvent the wheel. There is no "formula" into which they can plug their pixel intensities, plasma densities, and date of birth in order to churn out these magic numbers for them.

Here's the reason you need reproducibility. Imagine trying to estimate the force between two objects when you know only their mass. I.e., you have some measured value of force, $F_{\text{observed}}$, and you have a theory that goes like:

and we just keep plugging in guesses for the number $A$ until we stumble across the right one. This takes a very long time. Worst of all, if we take any other pair of masses in the universe, we find that

and now we have to go out and hunt for some magic number $B$ such that

which also takes a long time. Repeat for every single pair of masses ever. Never look for the pattern. But, after enough pain and effort, churn out numbers like $A$ and $B$ that arrive on-time for the paper. Repeat forever. Congratulations on your PhD!

If only we knew additionally that gravity was also related to relative separation between the masses, $r$, i.e.

and voila! Every time we look for $G$, we find that it actually has the same value (assuming we're in the Newtonian regime). Bravo! A universal (Newtonian) theory of gravity. Now, every time we have any two masses separated by any distance $r$, we don't need any other information. We can look up $G$ in a book, and it never changes, and we have a universal theory to point to.

It's ridiculous that, as physicists, we often do the former method rather than the latter. I can guarantee that many experimentalists, guilty of path A, will raise their hands and accuse me of being ridiculous. Randomly typing numbers into Python to get decent results from their experimental images is emphatically NOT the same thing as what I've described in the "gravity" example. "You have to be realistic," they'll say. "There's not enough time to find a good way to do most things. You can't possibly equate my approach to this absurd one."

But can't I? What is the operative difference? The truth is that my colleague-- otherwise a very competent physicist-- is guilty of nothing more than what many of our colleagues are guilty of- arbitrary choices taken simply to expedite the route to publication. If it works, leave it. So what if it only works because it's held together by duct tape and zip ties and good will? Results are results.

Results Aren't "Results"

Results are worthless if you can't contextualise them as part of some wider theory. Again, this is important in the pursuit of a methodology that isn't nonsensical, but also important as it forms the basis of the scientific method's central tenet: results have to be reproducible, verifiable, and grounded in evidence.

Getting something that works once isn't good enough. If we drive to the store in your Ford to get food, that's great. If, when we try to drive there a second time and find that the store is no longer there, this is unacceptable. Worse, imagine that every time we use your Ford, we have to go to your shed and use a different gearstick depending on the weather, your mood, and the day of the week. At any time on our trip to find the mythical vanishing store, the Ford might break down, too.

In cases like this, you can't treat the act of finally reaching the store as a success. The entire system that got us there is a cumbersome and ridiculous mockery of human existence, some vaudevillian parody of the scientific method. We need to find a way to locate the store, on demand, at any time, and we need a car that can run on the same fuel, with the same gearstick, on all days of the week.

The Car That Doesn't Break, and The Store That Doesn't Move

The ML Side of Things

We've taken a look at how we need well-defined end goals and equally well-understood, or at least quasi-justifiable, ways of getting there, and we need to be able to point to something concrete so that we don't have to resort to thumbing the scale, and plugging in random numbers until we get something that we "think" looks right. That's fitting the data to the conclusion-- not fitting the conclusion to the data.

I was technically a physicist (that's what it said on my DPhil). And I get a lot of flak from other students here at Oxf. for touting ML as a silver bullet (it's not, but it's at least chromium). But neural nets and machine learning ***are* physics**. They just are. Look no further than Restricted Boltzmann Machines² or the use of temperature in transformers^{3 4} and you'll see a whole lot of physics buried in there (not even that deep under the surface). Not to mention the fact that training the net is literally a clever application of calculus⁵, and we still sometimes use Newton's method for gradient descent in machine learning⁶. I'm dead serious. The man doesn't miss.

The man doesn't miss. Apart from when it came to relativity. Or alchemy. Or predictions of when exactly the world would end. His portrait watched me with empty eyes for all my four years as an undergrad.

I think the best justification for arguing that neural nets are a subset of physics-- and that, in fact, the best preparation you can get for designing and operating them is through a physics course-- is that you're studying a system governed by a differential equation. That, and a few other things. But I'll leave that for another post. I'll outline the two separate types of neural net that we're looking at combining in this project: convolutional neural nets and autoencoders, and at the end, you can tell me whether you think it'll work or not.

Convolutional Neural Networks

Convolutional neural networks (CNNs) have been around in one form or another for a very long time. The typical story goes something like this: in 1979, Fukushima proposed something called the Neocognitron⁷, inspired by earlier work concerning the receptive fields of cells in cat retinae⁸. A very smart person named Yan LeCun led a team at AT&T Bell Labs in the '80s and '90s to built a type of neural network capable of reading handwritten digits⁹ using a type of operation called convolution and which bore similarities to Fukushima's ideas.

CNNs are a powerful form of neural net that is often applied to image classification tasks, as was done famously during the 2012 ImageNet competition¹⁰, which revitalized the community's interest in using CNNs. A pretty OK summary of CNNs can be found here¹¹ (though it should be noted that this document has clearly not been proof-read) and Aggarwal's book¹² has an excellent (but more challenging) section on them.

Convolutional nets are, very basically, advantageous choices of architecture for image-classification due to their use of the eponymous convolution operation (though depending on who you ask, this might be better referred to as correlation¹³), which introduces a way of encoding relationships between neighbouring pixels, namely by passing a smaller matrix (a kernel-- remember how I told you we'd come back to it?) over the top of an image matrix and performing elementwise dot-products between the entries of the kernel and the image matrix. The advantage of this is that the subsequent number you get from this operation is influenced by several separate pixels in a certain neighbourhood of the original image (the size of the neighbourhood depending on the size of kernel). Note that you often reduce the dimensions of the matrix if you do this without padding the original image (add a bunch of 0 pixels around the edges). You can then do all different types of exciting things to this, including maxpooling, where you reduce the dimensions of the ''feature map'', which is what you produce in the convolution step, and keep only the cell with the biggest value. Among other things, these steps are useful in introducing translational invariance (a bird is a bird regardless of whether it is in the top right or bottom left of your image) and rotational invariance (a bird upside-down is a bird, etc.)

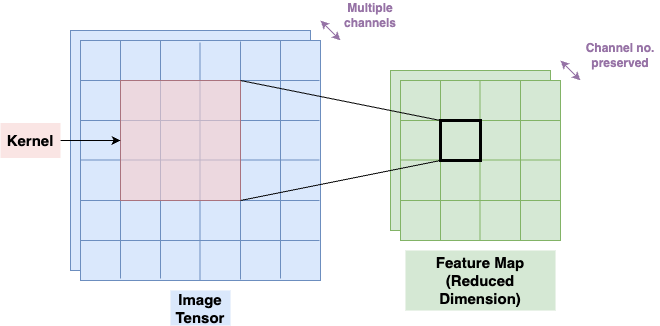
Simple schematic for convolution. Readers are advised to look literally everywhere else for a better diagram. Note that the number of "channels" is preserved, i.e. the kernel is applied separately to each of the channels, and so "depth" (channel number) is unchanged.

There is some encouraging evidence that CNNs can be supplemented or replaced as ML architectures for reading visual data by a Visual Transformer (Vi-T), which takes the technology used in modern LLMs to process input text and instead tasks it with processing an image, which has been divided into chunks¹⁴. These neural network can then learn relationships between these patches, much the same way a transformer in GPT learns relationships between words.

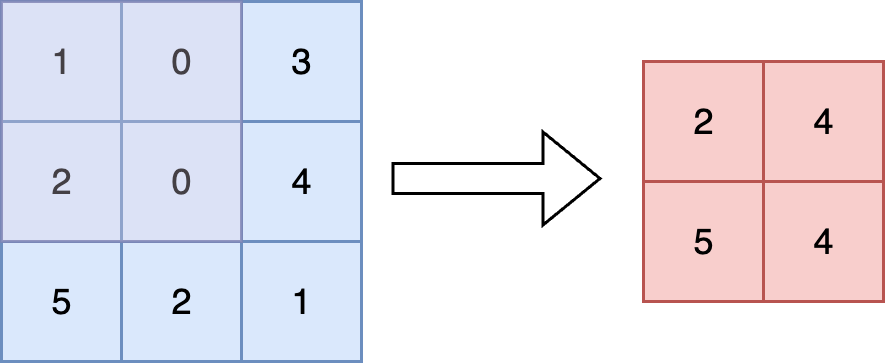
Maxpooling demonstrated with a kernel of dimensions 2x2. Note how this clearly reduces the size of the feature map. The original input is the blue matrix. The kernel is faint purple, and the output is the red matrix.

Autoencoders

Autoencoders are even more exciting than CNNs¹⁵, and are an important instance of where unsupervised learning is often implemented- we don't have tell the autoencoder what the data is, and we ask it to find features in the data by itself. It's pretty fascinating, and you can code up a simple one in less than an hour during an empty afternoon (I did it myself on MNIST¹⁶ here).

If we can force the neural network to compress the input data somehow without compromising on any of the important data (in the case of MNIST, this would be something like whether a digit is a 1 or a 7). Advantage: generalisable. There's a reason why my (scrawly, God-awful, STEM-student handwriting) 7s bear at least a passing resemblance to yours: there must be some deep, universal characteristics of the digit that can somehow be perceived in spite of the enormous variation between individuals' handwriting. For example, in a 7, it's probably not the orientation/rotation of the digit as a whole; more important is the fact that there are two straight lines, one horizontal and one vertical, at some rough relative angle, and not a lot of curviness¹⁷; compare to an 8 or a 2.

By squeezing the neural net in the middle, we essentially guarantee that there's a limit to the number of different features/characteristics the network can learn-- it can't retain every quirk of every single different person's 7-- it must learn some generalisable, universal features of what it means to be a number 7.

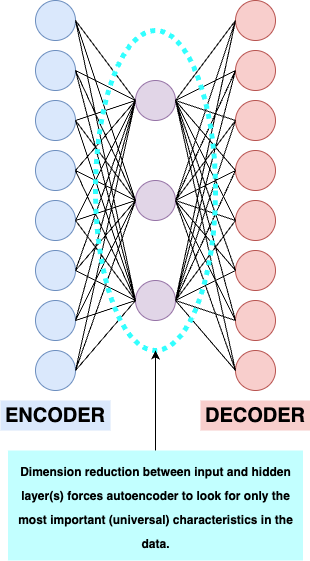
Schematic diagram of a simple autoencoder with only a single hidden layer

Autoencoders are impressive because they are able to do this while using the same old $MSE$ (mean squared-error) loss, which penalises any deviation from the original image (including the ignoring of any quirks in the handwriting). In theory, loss can be minimised to $0$ by reproducing the image pixel-by-pixel. But, again, it just can't do that if the number of nodes in the hidden layers is reduced compared to the input and output layers. It has to make sacrifices somewhere. Not to mention that if the model tries to adjust itself to minimise loss on a particularly weird (read: STEM-handwriting) image, it will pay the price by getting things very wrong on every other image- so catering to idiosyncrasies is ironed out by the optimisation process¹⁸.

This is great- but it's far harder to tell what's going on in a turbulent plasma than in handwritten digits (at least to the human eye)-- so how is this useful for plasma diagnostics? Well, in the same way that we force an autoencoder to ignore certain things about a digit, we might be able to force a more advanced neural network to ignore certain things about a noisy plasma image.

Best of Both Worlds- Convolutional Denoising Autoencoder (CDAE)

Ok- CNNs are good with images; check. Autoencoders have the capability of learning some reduced representation of images. So a convolutional autoencoder might have the ability to:

• (1) Recognise certain things about the image; e.g. regions of turbulence and interaction, jets, etc.
• (2) Realise that, if it's been forced to learn a small number of "rules" from which the image must be reconstructed, there are certain things that must be reproduced (the presence of a turbulence bright spot) and some things that aren't important enough to remember (where exactly the dead pixels are).

This is like training a robot that knows how to cut the mould out of bread. If you were asked to describe, in words and numbers, how precisely to cut out each piece of mould, from every slice of bread, regardless of shape, size, age, extent of mould growth, you'd find it hard. "Cut out the mould". OK. How do we know where the mould end and the bread begins? "The green stuff is mould". What is green? "OK, forget about it. Just cut around the shape of the mould". Is all mould the same shape? Damn.

But as humans we find it easy to cut out any amount of mould, regardless of shape, size, lighting, or knife choice. It's like we know mould when we see it. Indeed, "I know it when I see it" is a powerful form of human intuition that is lacking from machine learning. It's very hard to train artificial intelligence around this way of thinking; this is probably why we need to feed it so much data, when humans can identify mould after seeing it only once.

What we're doing here is training an algorithm that knows plasma when they see it. It doesn't matter what shape, brightness, or location the noise might appear in-- by forcing our network to learn reduced representations of images, we've forced it to only remember the attributes actually relevant to the plasma, rather than the noise.

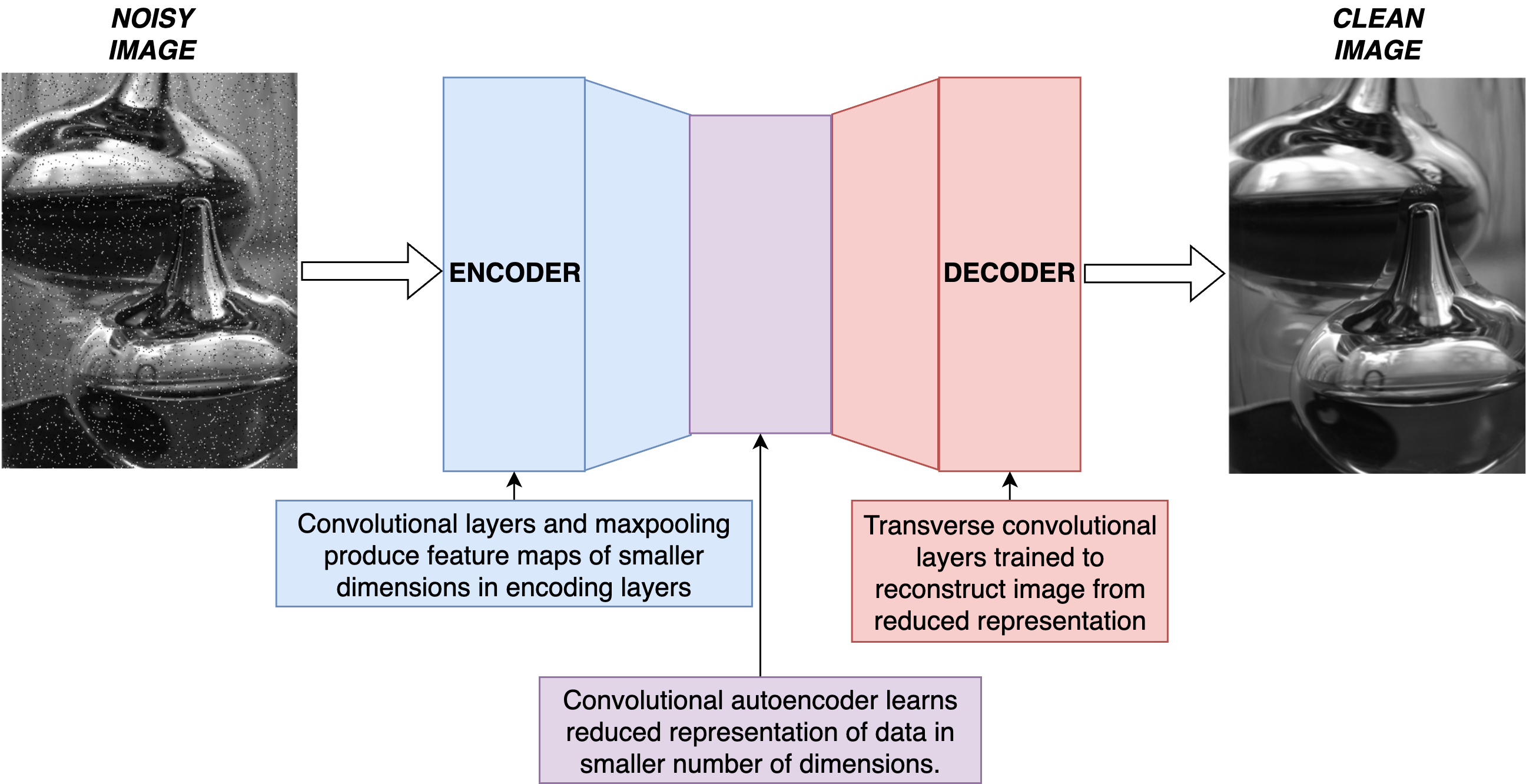
Schematic diagram of how these types of CDAEs work. Credit to myself and Luca Lorenzi.¹⁹

How does this address the "magic number" problem? Aren't we just replacing one set of random numbers-- before, the "threshold" values, chosen by hand-- for another (here, the neural network's weights and biases). No. The fact that we can't explain the exact value of a number isn't the determining factor. What matters is whether these values produce reproducible results. To a human, the number "123.4335235" typed somewhere in the dark corners of Python scripts looks as arbitrary as "$6.674\times {10}^{-11}{\text{m}}^3{\text{kg}}^{-1}{\text{s}}^{-2}$" (Newton's Gravitational Constant, $G$). The difference is that everyone can agree on the second number, and derive it over and over again, reproducibly, without any reliance on human preference. Not so for the first number. Changing it to "124.4335235" may produce data that "seems" acceptable to a second person. Who is to say which of them is right?

Furthermore, we have arrived at our set of numbers-- the weights and biases-- via the solution to a well-posed optimization problem. Our architecture is documented, and our optimization algorithm (some form of gradient descent) has well-defined steps that you can write out mathematically. Someone else with the same parameter initialization, GPU, dataset, and gradient descent scheme could recreate our results and confirm our results. Plus, we can look at how loss changes as training epoch increases-- is it tending to some constant value? We can train an ensemble of different models, and "fuse" them together, performing (for example) an average over their parameters, and look at the results those models produce. How do you even begin to justify averaging over the random numbers chosen by-eye in the depths of Pythonic binges?

There are a bunch of places where this type of filter would be useful, not least in the case where you have certain features in an image (e.g. sharp edges) with high-frequency components that would otherwise be removed by applying a Gaussian filter of arbitrary width. Similarly, changing your mode of median filtering until you have few enough speckles to please the eye fails to account for the possibility that those speckles are part of the image, and not just some sort of noise.

This feat has actually been achieved already this year in 2025 for simulated images produced using density functional theory (DFT) codes with some pretty impressive results²⁰. So, in short, the car has been built, and it works, so walking to the magic store on foot no longer makes any sense.

Application to Modern Physics

You may have your qualms with this approach. But, it can't be worse than what we currently have. At the moment, we essentially use a "one-size-fits-all" approach to filtering; keep in mind that your conventional filters are "trained" on a data set of size... 0. Regardless of the input data, we take it for granted that we can apply median filters, Gaussian filters... All without any real attempts to interrogate the data or understand what's going on viz. noisy data. In practice, much of the analysis is done only after the image has been (arbitrarily) filtered, when in fact there's quite a lot that a person could and should do beforehand.

It's true that modern experiments have a limited amount of shots to work with, so training them on actual data, while ideal, is not always going to be possible. Some points on that-- firstly, big physics installations are built to last for many experiments to be performed over many years. Because the facility has some set purpose(s), a lot of these experiments will be similar, and use the same devices. Furthermore, many people revisit the same facilities again and again, year after year, to reimplement the same experiments with incremental changes. This provides plenty of opportunities to train neural networks with convolutional substructures on at least the task of noise removal.

Secondly, most physics experiments are preceded by some form of simulation. They usually have to be in order to justify the expensive thing they're about to do at the facility which they're about to visit. My trips to CERN cost nothing- which is insane considering how we have access to the most sophisticated accelerator superstructure in the world, and considering how someone has to pick up that bill. Doing the science is free-- that was the whole point. But, if you're going to use something expensive and do it for free, there are other hoops to jump through, such as making your case to a scientific board regarding why you think your upcoming experiment is actually worth it. In this case, there is often a large dataset, somewhere, of simulated images on which you can presumably train some model, even noise them. In my [previous article] I talked about trying to train some sort of neural net to act as a surrogate for PIC simulations. This might take time, and it may take years to accumulate the necessary training data, but once it's done, it's done. You can always try and fine tune it later. If you're ambitious, you can look at making a physics-informed convolutional denoising auto encoder (PICDAE- not a handsome acronym).

Conclusions

As I've pointed out, this area of research is real, and active. People are working on surrogates, filters, and smart ways of doing things all the time. If you'd prefer to stick to the old methods then, well, there were also people who fought the introduction of AC current, too, and history was not kind to those people. Luddism and technophobia, in some formats, are deified in many academic or intellectual circles (just introduce yourself to an Oxford student with the line "I study AI" and let them run with the ball) where it's fashionable to be skeptical, critical, and existential about machine learning.

It's OK to be skeptical about new technology. A form of skepticism of the automobile is what brought us seatbelts and the electric vehicle, though maybe "skepticism" isn't the right world for this-- perhaps it's more like "limitation-" or "danger-consciousness". But regressing from the refrigerator to the ice house on account of how the former consumes more electricity is not a useful form of skepticism. Finding a way to built a more efficient refrigerator, however, is.

There are some tasks that certainly have to be offloaded to AI, and searching for random, optimal, twenty-four decimal place numbers is surely one of those tasks. Interfacing with raw numbers is not what humans are meant for-- that's why we write code symbolically in programming languages rather than in hexadecimal machine code (though some of you freaks reading this may still do that).

All experimental physicists can benefit from automating a lot of the process. Shouldn't we be happy about having more time to do more physics? Maybe, despite the hours of pain it inevitably will bring, digging about for those old hard-coded numbers in VSCode is at least familiar, and human beings often choose familiar problems over novel solutions.

Don't be human. Choose the car that doesn't break, and the store that doesn't move.